مصطلحات تقنية: كيف ترسم البطاقة الرسومية العالم ثلاثي الأبعاد ( 2 )؟
تحدثنا في مقالنا السابق عن الفكرة الأساسية التي تُبنى عليها المشاهد الرسومية ثُلاثية الأبعاد في الألعاب والمشاهد السينيمائية وأفلام الرسوم المتحركة ثُلاثية الأبعاد. وقد وصلنا وقتها لمعرفة المراحل الثلاثة الأساسية التي يتم بناء العالم ثُلاثي الأبعاد عليها وهي إنشاء عالم افتراضي ثلاثي الأبعاد. و تحديد أي جزء من العالم سيتم عرضه على الشاشة. وتحديد كيفية ظهور كل بكسل على الشاشة بحيث تظهر الصورة بأكملها بأكبر قدر ممكن من الواقعية . ولقد تناولنا بالفعل النُقطتين الأولين في المقال السابق. والآن دعونا نحول ناظرنا للنُقطة الثالثة وهي تحديد كيفية ظهور كل بكسل على الشاشة بحيث يظهر المشهد فعلياً بالشكل الواقعي الذي نراه أمامنا، لنعرف أخيراً كيف تقوم البطاقة الرسومية برسم المشاهد ثُلاثية الأبعاد على الشاشة !!...
![]()
بغض النظر عن حجم العالم الافتراضي ثلاثي الأبعاد أو ثرائه ، لا يمكن للكمبيوتر تصوير هذا العالم إلا من خلال تلوين وحدات البكسل على الشاشة ثنائية الأبعاد. لذا سيُركّز هذا القسم فقط على ما يفعله الرسامون التقنيون لجعل ما تراه على الشاشة يبدو واقعيًا ، وسنركز بشكل خاص على كيفية جعل المشاهد تبدو أقرب ما يمكن إلى ما تراه في العالم الحقيقي. سننظر أولاً في كيفية جعل كائن ثابت واحد يبدو واقعيًا . ثم سنُجيب على نفس السؤال للمشهد بأكمله مع مجموعة من الأجسام. وأخيرًا ، سننظر في ما يجب على الكمبيوتر فعله لعرض مشاهد بالحركة الكاملة للصور بشكل واقعي وبحركة واقعية.
في البداية، لابد لنا من التنويه إلى نُقطة هامة للغاية وهي أن المشهد ثُلاثي الأبعاد يدخل في تكوينه عدد من أجزاء الصورة المختلفة وذلك لجعل الكائنات تبدو حقيقية بشكل أكبر. من بين أهم هذه الأجزاء تأتي الأشكال نفسها والأنسجة أو ما نُسميه بالإكساءات، والإضاءة والمنظور الخاص بالمشهد، وعمق المجال، وممانع التعرجات. لذا فدعونا نأخذ هذه الأجزاء واحداً تلو الأخر بشكل بسيط..
الأشكال أو Shapes
لنفترض مثلاً أنك الآن قُمت بالنظر من خلال نافذة غرفتك، ما الذي تراه أماماك ؟. في الأغلب فأنت ترى الآن مشهد مكون من جميع أنواع الأشكال ، بعض الأجسام تبدو كخطوط مستقيمة ومنحنيات بأحجام وتركيبات عديدة. وبالمثل ، عندما ننظر إلى مشهد أو صورة رسومية ثلاثية الأبعاد على شاشة الكمبيوتر الخاصة بنا ، نرى صورًا مكونة من مجموعة متنوعة من الأشكال ، على الرغم من أن معظمها يتكون من خطوط مستقيمة في الأساس.... فنرى المربعات والمستطيلات ومتوازيات الأضلاع والدوائر والأشكال المعينية ، لكن الأهم من ذلك كله أننا نرى مثلثات.
قبل أن نبدأ في توضيح الفكرة دعونا في البداية نقوم بتوضيح بعض النقاط البسيطة لكي تتضح الصورة بشكل أكبر. علمنا مُسبقاً أن أي صورة أمامنا على الشاشة تتكون من مجموعة من الألوان التي تقوم الشاشة بعرضها عن طريق البيكسلات الموجودة عليها. لذا فيمكننا القول أن أي صورة تتكون بشكل أساسي من مجموعة من الألوان التي يتم تخزينها كما أشرنا سلفاً على شكل تكرارات للصفر والواحد (وذلك لأن الحاسب لا يفهم إلا هذه اللغة).
ولكن الصور التي تقوم الشاشة بعرضها ولكي تقوم برسم منظر طبيعي أو حتى شكل بسيط للغاية تتمتع بتناسق وترتيب مُعيّن لهذه الألوان أو الأشكال، وذلك لكي تظهر الصورة في كل مرة بنفس الشكل والأبعاد والألوان وما إلى ذلك. وذلك يعني ببساطة أن كل جسم يتمتع بمجموعة من الخصائص التي تُميزه أيّاً كان موقعه في الصورة (والقصد هنا سواء كان ثابت أو متحرك)، والسبب هو أن هذا الجسم يتم حفظ بياناته وأبعاده بشكل ما في ذاكرة الحاسب بحيث لا يحدث أي تشوه له بتغير موقعه.
دعونا نأخذ مثال

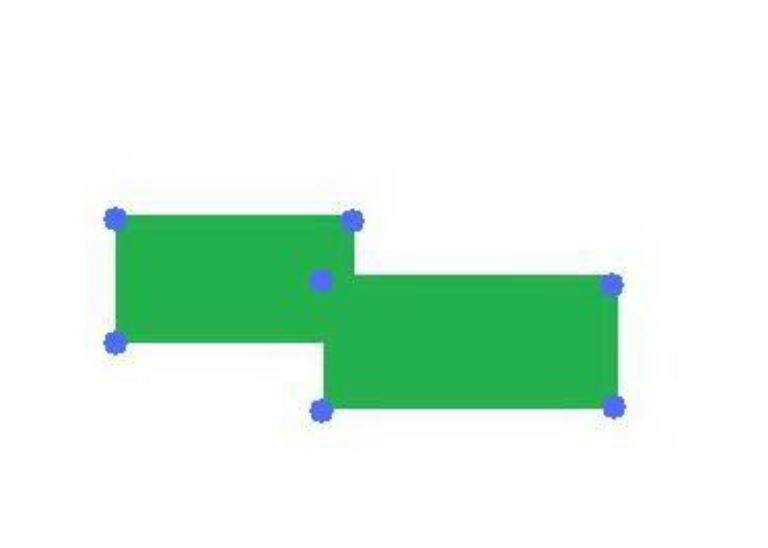
فعلى سبيل المثال دعونا نأخذ هذا الشكل في الأعلى كمثال، هل يمكنك التفرقة بين المستطيلين ؟ هل يمكنك معرفة أياً منهم في الأمام وأياً في الخلف ؟. في الأغلب لا أظن ذلك، وهي في الحقيقة ليست مهمتك كمستخدم أن تعرف ذلك أصلاً. ولكن في المقابل، فالحاسوب يجب عليه معرفة ذلك وتحديده حتى يقوم بإقناعك أنك تُشاهد مشهداً ثُلاثي الأبعاد. وذلك يعني أن الحاسب لابد وأن يجعل المشهد أقرب ما يكون للعالم الحقيقي ثُلاثي الأبعاد، أي أن لكل جسم طول وعرض وإرتفاع أو عمق، فيستقل بذلك كل جسم عن الجسم المجاور له من ناحية الخصائص لكي لا تتداخل الأجسام فيما بينها كما بينا في المقال السابق. ولكي يقوم الحاسب بهذه المهمة كان لابد من تطوير منظومة تُسمّى منظومة الرؤوس أو Vertex .

إنظر معي للشكل المستطيل الموجود في الأعلى، إذا لاحظت الآن ستجد أن الشكل أصبح مُحدد بأربعة نقاط أو رؤوس في كل زاوية. كل نقطة من هذه النقاط سنرمز لها برمز ما، وليكن ( أ ، ب ، ت ، ث ) مثلاً. الآن يمكننا تعريف هذا الشكل بهذه النقاط الأربعة. والآن وكما يظهر من الشكل التالي بعد التعديل (المستطيلين في الأسفل)، يمكننا الآن معرفة أي المستطيلين أمام الآخر، وذلك كما أشرنا بفضل الرؤوس التي قمنا بتعريفها. ولكن في عالم الحاسوب فالأمر سيكون أكثر تعقيداً من هذا الشكل البسيط، كما أن هذه النقاط سيتم تخزينها في ذاكرة الحاسب كما نعلم بإستخدام تكرارات الصفر والواحد. المشكلة الوحيدة هنا أن هذا الشكل ثُنائي الأبعاد، وكما أشرنا في البداية فنحن هنا نتحدث عن العالم ثُلاثي الأبعاد. لذلك فالرسوم ثُلاثية الأبعاد في الحاسب يتم تعريف كل نقطة فيها بثلاثة أبعاد وليس بُعدين فحسب لكي نستطيع رسم المشاهد بشكل قريب من الواقع (طول /عرض /وعمق).
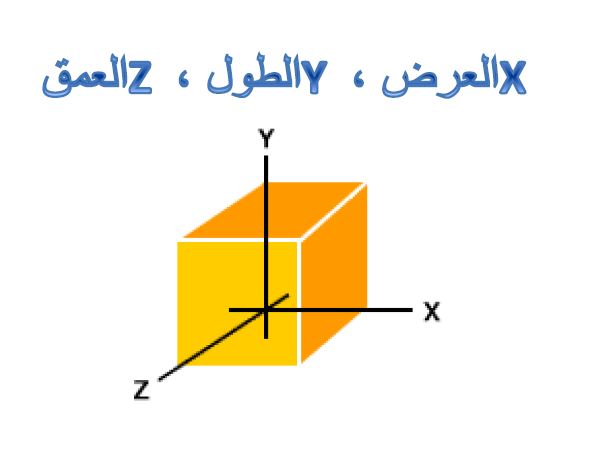
ومن هنا يأتي تعريف الرؤوس ثُلاثية الأبعاد، فكل نُقطة أو رأس تتمتع بقيمة لمكانها على المحور السيني (محور X) وقيمة لمكانها على المحور الصادي (محور Y) ، وقيمة على محور Z الذي يُعبّر عن العمق أو السُمك. لذا فببساطة الرؤوس أو الـ Vertex هي نقاط موجودة داخل الأشكال التي تظهر أمامنا على الشاشة، ولكنها تتمتع بثلاثة قيم للمحاور الثلاثة يتم تخزينها في ذاكرة الحاسب .

ولتوضيح ذلك بشكل أكبر دعونا نأخذ مثال بسيط. لنفترض أننا أمام خط يتكون من نُقطتين متصلتين هما (أ) و (ب). هاتين النُقطتين كما أشرنا سيتم تعريف كل واحدة منهم بثلاثة قيم ولتكن مثلاً قيم النُقطة الأولى (أ) هي القيم التالية (3،4،5) بحيث تكون 5 هي قيمة المحور X و 4 هي قيمة المحور Y و 3 هي قيمة المحور Z . والرأس الثاني أو النُقطة الثانية (ب) سيكون لها مثلاً القيم التالية (6،8،5) لنفس المحاور بالطبع . الآن يمكننا بوضوح أن نرى أن كل نُقطة أو رأس أصبح له قيمة في العالم ثُلاثي الأبعاد، ولكي يتم تحريك هذا الخط كما هو لليمين أو اليسار أو حتى لأي زاوية كانت، فالأمر سيكون بسيطاً للغاية، وسيقوم مُعالج يُسمّى Vertex Processor بالقيام بهذه العملية.
كُل ما في الأمر هو أن هذا المعالج يقوم بعملية جمع وطرح لتحريك هذا الخط، فكيف ذلك ؟
دعونا نفترض مثلاً والفرض هُنا جدلي للغاية ولا يُمثل المشهد الذي يحتوي على ملايين النقاط والأشكال، ولكننا سنقوم بتبسيط الأمر لكي تفهم الفكرة. حسناً، لنفترض أن هذا الخط هو الشخصية التي تقوم بتحريكها داخل لُعبة ما مثلاً، فأنت عندما تضغط بزر لوحة المفاتيح ضغطة واحدة لليمين مثلاً ستقوم لوحة المفاتيح بتمرير الأمر للمعالج ومنه للبطاقة الرسومية التي سيقوم مُعالج الرؤوس بداخلها بتطبيق هذه الحركة على الشكل الذي أمامه أو الشخصية في داخل اللعبة. وكما إفترضنا للتو فالشخصية التي تلعب أنت بها الآن هي ذلك الخط الذي يتكون من النقطتين (أ) و (ب).

سيقوم مُعالج الرؤوس الآن بحساب قيمة هذه الضغطة وتحويلها لإحداثيات، ولتكن مثلاً هذه الضغطة سريعة وبسيطة للغاية، لذلك فيُترجمها معالج الرؤوس لقيمة 5 على المحور الرأسي أو محور X مثلاً (قيمة الحركة هُنا فرضية أيضاً). هذه الحركة التي بمقدار 5 درجات على محور الـ X سيتم تطبيقها الآن على الجسم أو الخط المستقيم، فيتم زيادة 5 نقاط لقيمة الـX الخاصة بالنُقطة (أ) فتُصبح القيمة الجديدة هي (3،4،10) وتُصبح قيمة النُقطة (ب) الجديدة بعد الحركة هي (6،8،10) . لذلك فكما ترى كُل ما في الأمر أن المعالج قام بجمع قيمة الحركة وأضافها على القيم الخاصة بكل نُقطة في الجسم الذي أمامه.
وكما ترى أمامك يا صديقي فالخط الأحمر نفسه تحرك أيضاً، والسبب ببساطة هو أن الرؤس الخاصة به تحركت، وهي التي تُحدد الهيكل الخارجي لهذا الخطة، ولذلك فمنظمة الرؤوس توفر الكثير من الجهد، فبدلاً من أن تقوم البطاقة الرسومية بتحريك كُل نُقطة في الخطة، فهي تقوم بتحريك الرؤوس فحسب فيتحرك معها الشكل بالكامل....
والآن أصبح بإمكان المعالج الرسومي التحكم في هذا الخط لتحريكه لليسار أيضاً عن طريق جمع قيمة سالبة، أو تحريكه للأعلى والأسفل وذلك عن طريق تغيير قيم محور Y ، أو تقريبه من الشاشة (تكبيره) أو إبعاده عنها (أي يُصبح أصغر) عن طريق تغيير قيم المحور Z...الأمر غاية في البساطة أليس كذلك ؟!...في الحقيقة الإجابة هي نعم ولا، فالعملية في حد ذاتها ليست مُعقدة للغاية ولكنها مع المشاهد الغزيرة بالأجسام ثُلاثية الأبعاد تكون مُكلّفة للغاية وسأقوم بتوضيح ذلك حالاً، فلا داعي للتوتر صديقي العزيز.
البُعد الرابع !!
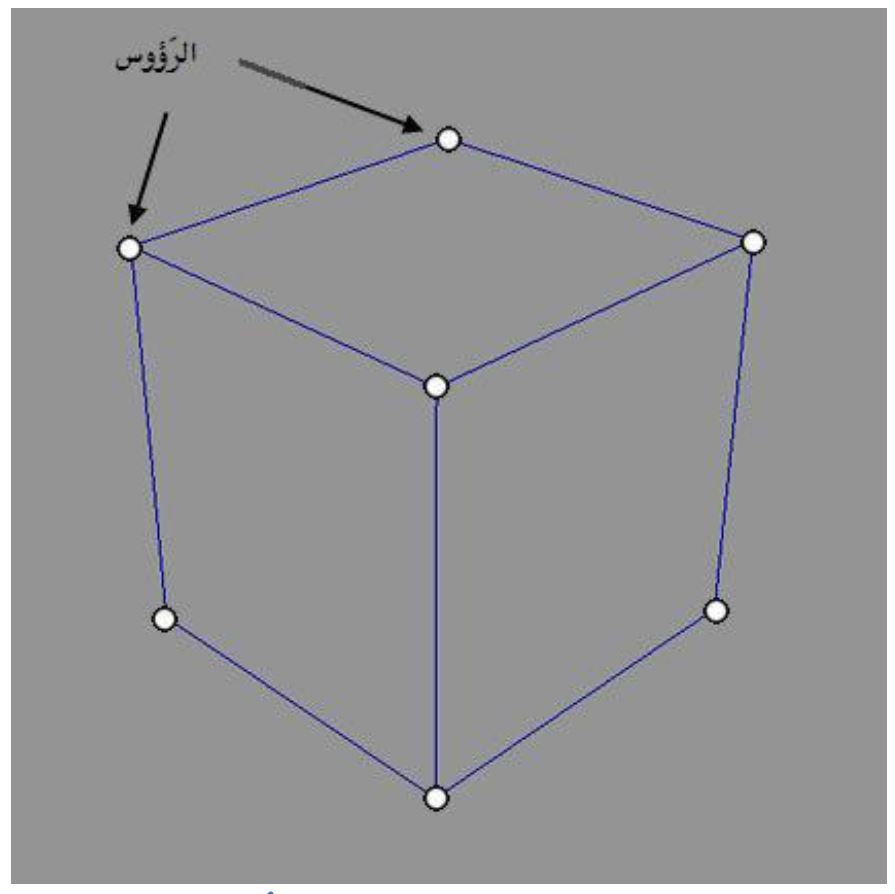
أضاف المطورون بعد ذلك بُعداً رابعاً لهذه الرؤوس والذي تم تسميته بالوزن أو Weight. وهو يعني وزن الرأس وقابليته للحركة ، لتُصبح الرؤوس الآن تتكون من X و Y و Z و W ...والآن يمكننا أخيراً فهم أن جميع الأشكال ثُلاثية الأبعاد تتكون من مجموعة من الرؤوس التي يتم توصيلها ببعضها للحصول على هذه الأشكال، النُقطة الهامة هُنا هو أن عملية الرسم نفسها يدخل فيها مبادئ الرسم الحقيقي (والمقصود بالرسم الحقيقي هُنا هو الرسم الذي يقوم به الرسامون في الحقيقة على اللوحات الورقية)، حيث تُصبح الأجسام البعيدة أصغر والأجسام الطويلة أقل سماكة في الأجزاء الأبعد وما إلى ذلك (هذا المُكعّب يُمثّل الفكرة، حيث أن الضلوع الأبعد تظهر أقل سماكة) .
يتم حفظ قيم هذه الرؤوس في الذاكرة مثلها كالألوان تماماً، وتقوم البطاقة الرسومية عند الحاجة لإستدعاء هذه القيم لرسم هذه الأشكال أو التحكم فيها وتحريكها بشكل ما. ولكن كما نعلم جميعا، فالعالم الإفتراضي لا يقتصر على الحركة فحسب، ولذلك فالبطاقة الرسومية تتولى تنفيذ مجموعة متنوعة من العمليات على هذه الرسوميات غير تحريكها. فعلى سبيل المثال، قد تقوم البطاقة بتغيير الأشكال، أو إضافة إنبعاجات أو زيادة أجزاء، أو حتى تدمير بعض الأجسام كما يحدث في حالات الإنفجارات أو دخول أجسام داخل أجسام أُخرى وإختراقها وما إلى ذلك من التغييرات التي تحدث على الرسوم.
وهذا كُلّه يحتاج تحكم أكبر من البطاقة الرسومية في تلك الأشكال، وليس فقط حدود هذه الأشكال . ولذلك فهذه الأشكال في الأغلب تحتوي على مجموعة من الرؤوس الفرعية داخل هذه الأجسام وليس فقط الرؤوس التي تُحدد حدود هذه الأجسام. لذا فمع هذه الرؤوس الفرعية ستتوفر لدى البطاقة الرسومية الآن القُدرة على تغيير أو تكسير جُزء ما من المكعب الذي لدينا في الأعلى مثلاً أو تغييره بشكل ما. هذه الرؤوس الداخلية في الأجسام انبثق منها بعد ذلك ما يُسمّى بنظام المُضلّعات أو Polygons .
ما هو نظام المُضلّعات Polygons ؟
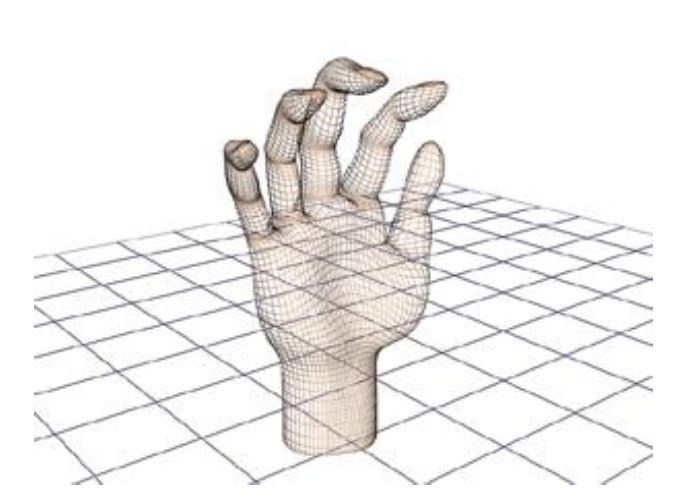
نظام المُضلّعات كما أشرنا في المثال السابق يقوم على مبدأ بسيط للغاية، وهو أن كُل الأجسام التي يتم رسمها داخل الحاسب تتكون من مجموعة من الأجسام الأصغر، والتي تسمع بالتحكم في الشكل الأكبر بسهولة وسلاسة أكثر. يمكنك الآن مثلاً النظر إلى تلك اليد المرسومة أمامك، ما الذي تُلاحظه ؟ ستُلاحظ أن اليد تتكون من مجموعة كبيرة من الأشكال الأصغر مثل المُربعات والمُستطيلات الصغيرة ، والتي تتجمع في النهاية لتكوين الجسم ثُلاثي الأبعاد.
هذه اليد يُمكن التحكم تقريباً في كُل جزء أو مُضلّع بداخلها على حدة، وذلك بسبب تلك المُضلعات المتعددة، حيث يُمكنك تلوين بعض المُضلعات بألوان والبعض الأخر بألوان أُخرى أو وضع بعض الرتوش على اليد وما إلى ذلك من التحكم الذي سيكون أكثر دقة من أن تكون اليد متكونة من مجموعة من الرؤوس التي تُحدد الحدود الخارجية فحسب (ففي حالة تم رسم اليد عن طريق تحديد حدودها الخارجية فقط فأنت لا تستطيع التحكم في كُل ما في داخل هذه اليد مثل الكفة أو الأصابع مثلاً !!) .
فكل خلية أو مُضلّع في تلك اليد يتكون من مجموعة من الرؤوس المتشابكة التي تُحدد حدود كل مُضلّع.
ولكن هناك سؤال قد يطرح إلى بالك عزيزي القارئ (في حال كنت لا تزال معي بالتأكيد) وهو هل يمكننا أن نجعل المُربعات هي الشكل أو المعيار العالمي والرسمي للمضلعات ؟ هل يُمكننا رسم جميع الأجسام التي نُريدها بمنحنايتها وزواياها بإستخدام المُربعات فحسب ؟. الإجابة ببساطة هي "لا"، فهناك بعض الأشكال مثل الدوائر والمُنحنيات مثلاً التي لا تستطيع الحصول عليها بإستخدام المربعات. ومن هُنا تم إستبدال هذه المُربعات بالمُثلثات لتُصبح هي الشكل الأساسي للمُضلعات، فبإستخدام المُثلثات يستطيع المطورون رسم أي شكل يُريدونه تقريباً وأي منحنيات تخطر على بالهم.
والآن، مع نظام المُضلّعات سواء كان المطور يستخدم المُضلّعات التي على شكل مثلثات أو مستطيلات ومربعات، فعملية التحكم في الأشكال ثُلاثية الأبعاد أصبحت أكثر مرونة ودقة، يمكن الآن للمطور التعديل وتلوين أجزاء من هذه الأشكال والتحكم في أبعادها وتغييرها وما إلى ذلك، أيّا كانت هذه الأشكال، سواء كُنّا نتحدث عن سيارة أو شخص أو حتى جبل. ولكن كل هذه العمليات تحتاج الكثير من قوى المعالجة وهو ما يجعل البطاقة الرسومية تحتوي على مجموعة من المُعالجات المُتخصصة في الجمع والطرح لكل من تلك العمليات التي تتم الرؤوس الخاصة بهذه الأشكال (كما ذكرنا مع مثال الخط الأحمر) .
ومع إستخدام أسلوب المُضلعات في رسم الأشكال، أصبح الشكل الواحد يحتوي على الآلاف من الرؤوس ، وأصبح المشهد أو الصورة الواحدة التي تتم عرضها تحتوي على الملايين من الرؤوس في نفس الصورة، وهو ما يعني الحاجة لمُعالجات غاية في القوة لتستطيع التعامل مع كل هذه الرؤوس وأدآء آلاف العمليات الحسابية في الثانية الواحدة. هذه العمليات التي تتم على الرؤوس تُسمّى تنصيب الرؤوس أو Vertex Setup ، وتقوم بهذه العمليات مُعالجات مُخصصة تُسمّى معالجات الرؤوس Vertex processors (سابقاً)، ولكنها الآن يُمكن القيام بها من خلال مُعالجات التظليل أو الـ Shader Processors العادية.
عملية رسم الخطوط
دعني أقول لك عزيزي القارئ على سر كبير، وهي أن الأشكال ثُلاثية الأبعاد لا تتواجد إلا على هيئة مجموعة من الرؤوس داخل معالجات التظليل فقط. نعم، رؤوس بدون أية خطوط تقوم بتوصيل هذه الرؤوس ببعضها البعض، والسبب هنا هو أن البطاقة الرسومية تطلب من هذه المعالجات وظيفة واحدة لتقليل عبء العمل عليها، ولذلك فهي تتولى فقط التحكم في هذه الرؤوس وتحريكها وتغيير مواقعها وما إلى ذلك من العمليات التي تتم على هذه الرؤوس.
لذا وبعد أن تنتهي هذه المعالجات من تحريك والتحكم في الرؤوس، تقوم البطاقة الرسومية بعد ذلك بتوصيل هذه الرؤوس ببعضها في عملية تُسمى عملية التوصيل أو Interpolation، والتي تجعلك تتذكر لعبة توصيل النقاط التي كُنّا نلعب بها عندما كُنّا صغاراً. وبشكل سريع وبدون الغوص في تفاصيل هذه النقطة، فعملية التوصيل تعتمد على مبادئ ما يُسمّى بعلم التوصيل والذي يهتم بمعرفة الطريقة الأمثل لتوصيل مجموعة من النقاط التي لا يربطها رابط، ويتم ذلك عن طريق رسم خطوط من خلال البيكسلات الموجودة على الشاشة طبعاً. (النقاط الحمراء هي الرؤوس والخطوط الزرقاء هي البيكسلات التي تم توصيلها).
ولكي لا تحدث مشاكل أثناء عملية التوصيل، تقوم البطاقة الرسومية في العادة بإستخدام الذاكرة الرسومية الخاصة بها أو ذاكرة النظام كمرجع لها لتقوم بتوصيل الرؤوس بشكل صحيح لتكوين المُضلّعات ومن ثم الشكل النهائي كما في حالة صورة الوجه الذي أمامنا هنا. حيث أن هذا الوجه كان في البداية مجموعة من الرؤوس فحسب، ولكن تم توصيلها بإستخدام المعالج الرسومي لتتكون المُضلّعات التي توضح لنا الشكل النهائي كما نرى.
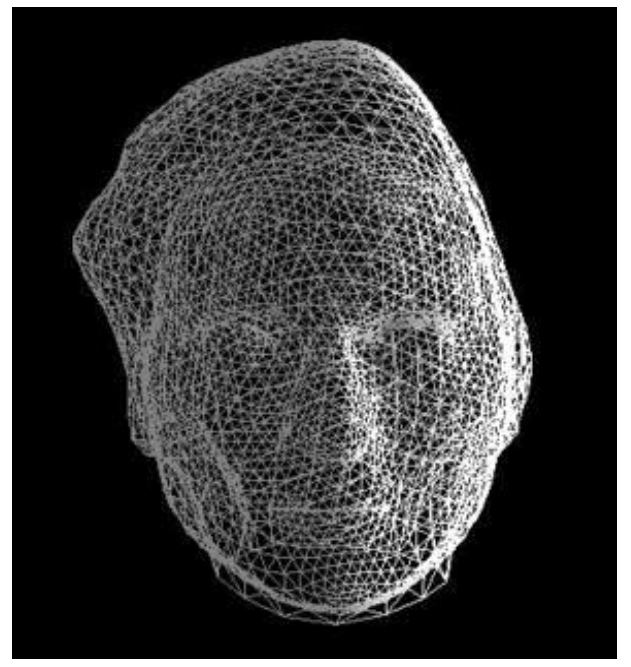
الخطوة التالية الآن هي عملية التلوين، وهنا يتم تلوين جميع المُضلّعات الداخلة في تكوين الشكل كُلٌ على حدة حسب ما تم حفظه أيضاً في الذاكرة الخاصة بالجهاز أو البطاقة الرسومية. وتبدأ عملية التلوين من حواف المُضلّع وللداخل كما في الصورتين التاليتين، حيث تم في الأول تلوين الحواف باللون الأزرق، ومن ثم الجسم الداخلي للمُضلّع. وبعد ذلك تتنقل البطاقة للمُضلّع التالي وهكذا حتى يتم تلوين الشكل والمشهد بالكامل في جزء من الثانية.
ملحوظة: عملية التلوين في البطاقة الرسومية تتم بإستخدام دقة 24bit ، وهي الدقة التي يتم تسجيل الألوان بها، وتسمح بدورها بتكوين ما يصل إلى 16 مليون لون، هم حصيلة إختلاط الألوان الثلاثة الأساسية مثل الأزرق والأخضر والأحمر RGB . وفي الوقت الحالي تمت إضافة درجة أُخرى فوق هذه الدقة وهي 8bit التي تسمح لوجود الشفافية في الألوان Alpha compostion، التي تسمح برسم المياه والزجاج والأجسام الشفافة الأُخرى، لتُصبح الألوان الآن بدقة 32bit وتُسمى RGBA .
عملية التلوين نفسها تُسمّى Rasterization و كانت تقوم بها معالجات النقاط أو البيكسلات أو Pixel processors (في السابق)، ولكن الآن تقوم بها مُعالجات التظليل أو Shader processors في البطاقات الأحدث.
ملخص ما ذكرناه
كما أشرنا اليوم، من أجل بناء صور تبدو كما لو كانت تحتوي على منحنيات سلسة كتلك التي توجد غالبًا في الطبيعة ، يجب أن تكون بعض الأشكال التي يتم بناء الأجسام الموجودة في الصورة صغيرة جدًا ، وقد تتطلب الصورة المعقدة - على سبيل المثال ، مثل جسم الإنسان - الآلاف من هذه الأشكال والخطوط أو المُضلعات التي يتم تجميعها معًا في هيكل يسمى الإطار السلكي. في هذه المرحلة ، قد يكون من الممكن التعرف على الهيكل باعتباره رمزًا لما ستصوره في النهاية ، ولكن الخطوة الرئيسية التالية المهمة هي : أنه يجب إعطاء الإطار السلكي سطحًا.
فبالنسبة لتلك الأشكال التي تكلمنا عنها في الأعلى، لاتزال جميعها لا تتمتع بقوام كذلك الموجود في العالم الحقيقي، أليس كذلك ؟!!.
ولعل السبب الرئيسي وراء ذلك هو أمر وحيد، فنحن لازلنا أمام شاشة الحاسوب، وهو ما يعني أن جميع المعلومات التي لدينا هي فقط تلك التي نراها، ويجب علينا أن نقوم بإستنباط جميع المعلومات من خلال ما نراه فقط. فعلى سبيل المثال، يمكنك معرفة قوام سطح ما في العالم الحقيقي من خلال اللمس، أو من خلال النظر إليه من مجموعة من الزوايا....لذلك وعلى النقيض وفي العالم الرسومي، يمكننا فقط النظر إلى السطح للحصول على جميع المعلومات الممكنة .
وهذه المعلومات تنقسم إلى ثلاثة مجالات أو أقسام :
أولاً اللون : ما هو لون الشكل الذي أمامي ؟ هل يتمتع الشكل بنفس اللون في كل مكان ؟
الملمس: هل يبدو الجسم أملسًا أم به خطوط أو نتوءات أو حفر أو بعض المخالفات الأخرى على السطح؟
الانعكاس: ما مقدار الضوء الذي يعكسه الجسم ؟ هل تبدو انعكاسات العناصر الأخرى على السطح حادة أم ضبابية؟
تتمثل إحدى الطرق التي يتبعها المصممون في جعل الصورة تبدو "حقيقية" بشكل أكبر في الألعاب، في الحصول على مجموعة متنوعة من هذه الميزات الثلاث وتطبيثها عبر أجزاء مختلفة من الصورة. ولأُعطيك مثال، انظر حولك الآن : ستجد أن لوحة المفاتيح الخاصة بك لديها لون / نسيج / انعكاس مختلف عن سطح المكتب الخشبي مثلاً ، والذي بدوره يتميز بلون / نسيج / انعكاس مختلف عن ذراعك، وهكذا .
ومن هنا تبدأ عملية تطبيق هذه الخطوات الثلاثة على المُضلعات أو الهيكل الخاص بالرسوميات التي تحدثنا عنه للتو. فللحصول على ألوان واقعية ، من المهم أن يتمكن الكمبيوتر من الاختيار من بين ملايين الألوان المختلفة لوحدات البكسل المكونة للصورة بدقة كبيرة. وفي المقابل، يأتي التنوع في الملمس أو النسيج من خلال النماذج الموجودة للأسطح والتي تتراوح من جلد الضفدع إلى الصخور وأوراق الأشجار، وتلك الأنسجة أو الإكساءات كما نُطلث عليها في عالم الرسوميات تكون موجودة داخل "خرائط النسيج" المخزنة التي يتم تطبيقها على الأسطح بعد ذلك.








